Is this packing of three squares in a circle optimal?
11
Ṁ938Dec 31
97%
chance
1D
1W
1M
ALL
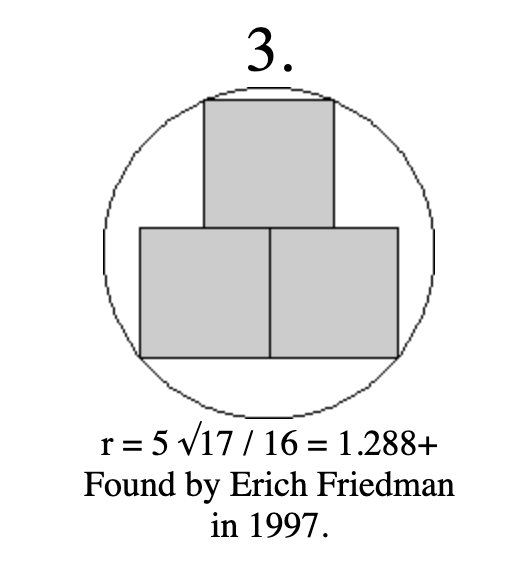
Via https://erich-friedman.github.io/packing/squincir/
Is the depicted configuration optimal, in the sense that it gives the smallest radius circle in which three unit squares can be packed?
Market to be extended until a proof is provided.
Get Ṁ1,000 play money
Sort by:
@JussiVilleHeiskanen Seems to me it's pretty much the same terminology as you use in /JussiVilleHeiskanen/is-the-best-packing-of-squares-insi
If I "pack" a bunch of suitcases into the back of a car, then the space taken up by different suitcases can't intersect.